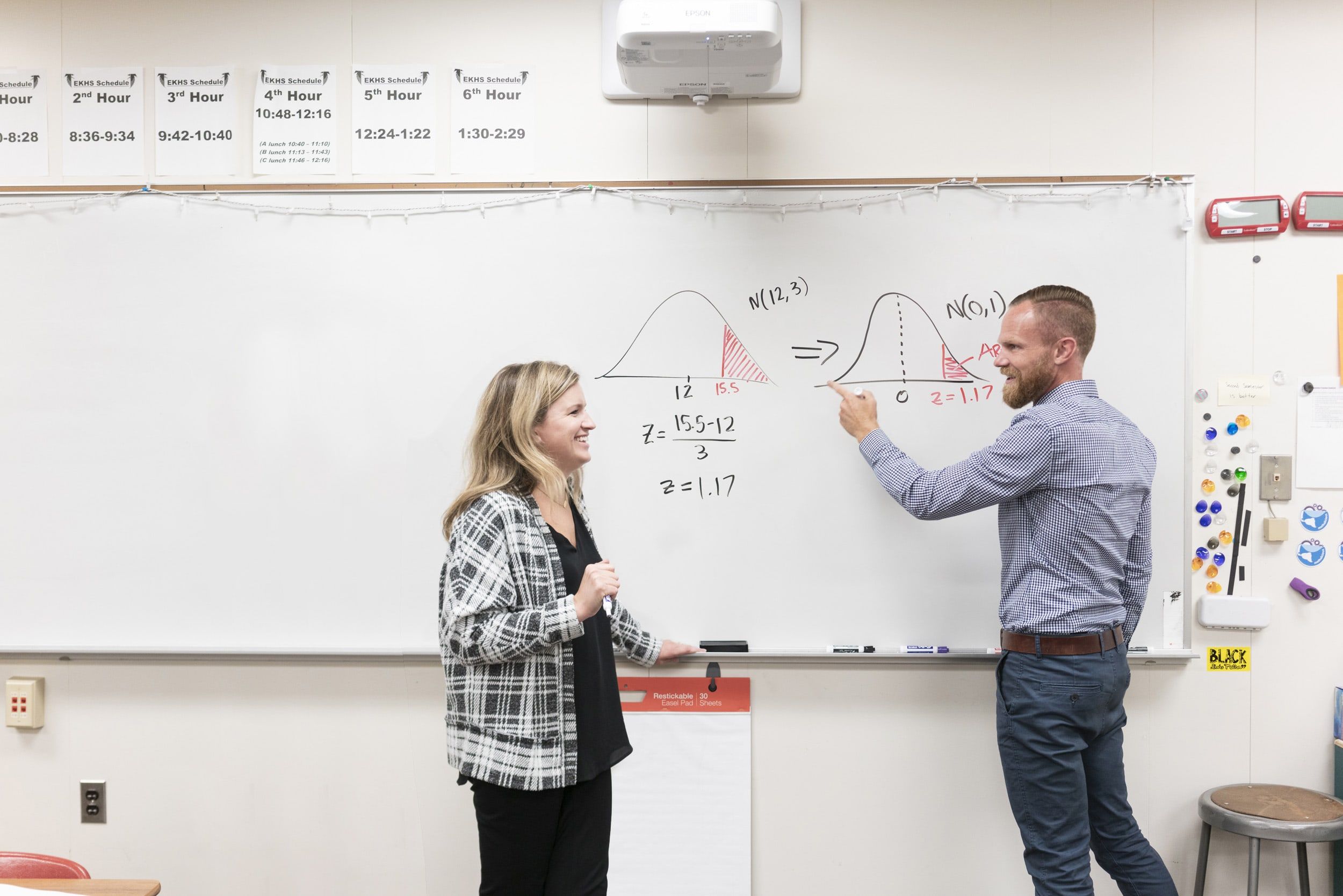
Our Teaching Philosophy
Experience First, Formalize Later
Every lesson begins with students working collaboratively in small groups through a sequence of carefully crafted questions that slowly build in complexity (Experience First). Following this activity, the teacher facilitates a discussion connecting students’ ideas with academic vocabulary and notation (Formalize Later). This approach encourages students to build strong math identities and take an active part in mathematical sense-making.