
Areas of Quadrilaterals (Lesson 5.5)
Unit 1: Reasoning in Geometry
Day 1: Creating Definitions
Day 2: Inductive Reasoning
Day 3: Conditional Statements
Day 4: Quiz 1.1 to 1.3
Day 5: What is Deductive Reasoning?
Day 6: Using Deductive Reasoning
Day 7: Visual Reasoning
Day 8: Unit 1 Review
Day 9: Unit 1 Test
Unit 2: Building Blocks of Geometry
Day 1: Points, Lines, Segments, and Rays
Day 2: Coordinate Connection: Midpoint
Day 3: Naming and Classifying Angles
Day 4: Vertical Angles and Linear Pairs
Day 5: Quiz 2.1 to 2.4
Day 6: Angles on Parallel Lines
Day 7: Coordinate Connection: Parallel vs. Perpendicular
Day 8: Coordinate Connection: Parallel vs. Perpendicular
Day 9: Quiz 2.5 to 2.6
Day 10: Unit 2 Review
Day 11: Unit 2 Test
Unit 3: Congruence Transformations
Day 1: Introduction to Transformations
Day 2: Translations
Day 3: Reflections
Day 4: Rotations
Day 5: Quiz 3.1 to 3.4
Day 6: Compositions of Transformations
Day 7: Compositions of Transformations
Day 8: Definition of Congruence
Day 9: Coordinate Connection: Transformations of Equations
Day 10: Quiz 3.5 to 3.7
Day 11: Unit 3 Review
Day 12: Unit 3 Test
Unit 4: Triangles and Proof
Day 1: What Makes a Triangle?
Day 2: Triangle Properties
Day 3: Proving the Exterior Angle Conjecture
Day 4: Angle Side Relationships in Triangles
Day 5: Right Triangles & Pythagorean Theorem
Day 6: Coordinate Connection: Distance
Day 7: Review 4.1-4.6
Day 8: Quiz 4.1to 4.6
Day 9: Establishing Congruent Parts in Triangles
Day 10: Triangle Congruence Shortcuts
Day 11: More Triangle Congruence Shortcuts
Day 12: Practicing the Triangle Congruence Shortcuts
Day 13: Triangle Congruence Proofs
Day 14: Triangle Congruence Proofs
Day 15: Quiz 4.7 to 4.10
Day 16: Unit 4 Review
Day 17: Unit 4 Test
Unit 5: Quadrilaterals and Other Polygons
Day 1: Quadrilateral Hierarchy
Day 2: Proving Parallelogram Properties
Day 3: Properties of Special Parallelograms
Day 4: Coordinate Connection: Quadrilaterals on the Plane
Day 5: Review 5.1-5.4
Day 6: Quiz 5.1 to 5.4
Day 7: Areas of Quadrilaterals
Day 8: Polygon Interior and Exterior Angle Sums
Day 9: Regular Polygons and their Areas
Day 10: Quiz 5.5 to 5.7
Day 11: Unit 5 Review
Day 12: Unit 5 Test
Unit 6: Similarity
Day 1: Dilations, Scale Factor, and Similarity
Day 2: Coordinate Connection: Dilations on the Plane
Day 3: Proving Similar Figures
Day 4: Quiz 6.1 to 6.3
Day 5: Triangle Similarity Shortcuts
Day 6: Proportional Segments Between Parallel Lines
Day 7: Area and Perimeter of Similar Figures
Day 8: Quiz 6.4 to 6.6
Day 9: Unit 6 Review
Day 10: Unit 6 Test
Unit 7: Special Right Triangles & Trigonometry
Day 1: 45˚, 45˚, 90˚ Triangles
Day 2: 30˚, 60˚, 90˚ Triangles
Day 3: Trigonometric Ratios
Day 4: Using Trig Ratios to Solve for Missing Sides
Day 5: Review 7.1-7.4
Day 6: Quiz 7.1 to 7.4
Day 7: Inverse Trig Ratios
Day 8: Applications of Trigonometry
Day 9: Quiz 7.5 to 7.6
Day 10: Unit 7 Review
Day 11: Unit 7 Test
Unit 8: Circles
Day 1: Coordinate Connection: Equation of a Circle
Day 2: Circle Vocabulary
Day 3: Tangents to Circles
Day 4: Chords and Arcs
Day 5: Perpendicular Bisectors of Chords
Day 6: Inscribed Angles and Quadrilaterals
Day 7: Review 8.1-8.6
Day 8: Quiz 8.1 to 8.6
Day 9: Area and Circumference of a Circle
Day 10: Area of a Sector
Day 11: Arc Length
Day 12: Quiz 8.7 to 8.9
Day 13: Unit 8 Review
Day 14: Unit 8 Test
Unit 9: Surface Area and Volume
Day 1: Introducing Volume with Prisms and Cylinders
Day 2: Surface Area and Volume of Prisms and Cylinders
Day 3: Volume of Pyramids and Cones
Day 4: Surface Area of Pyramids and Cones
Day 5: Review 9.1-9.4
Day 6: Quiz 9.1 to 9.4
Day 7: Volume of Spheres
Day 8: Surface Area of Spheres
Day 9: Problem Solving with Volume
Day 10: Volume of Similar Solids
Day 11: Quiz 9.5 to 9.8
Day 12: Unit 9 Review
Day 13: Unit 9 Test
Unit 10: Statistics and Probability
Day 1: Categorical Data and Displays
Day 2: Measures of Center for Quantitative Data
Day 3: Measures of Spread for Quantitative Data
Day 4: Quiz Review (10.1 to 10.3)
Day 5: Quiz 10.1 to 10.3
Day 6: Scatterplots and Line of Best Fit
Day 7: Predictions and Residuals
Day 8: Models for Nonlinear Data
Day 9: Quiz Review (10.4 to 10.6)
Day 10: Quiz 10.4 to 10.6
Day 11: Probability Models and Rules
Day 12: Probability Using Two-Way Tables
Day 13: Probability Using Tree Diagrams
Day 14: Quiz Review (10.7 to 10.9)
Day 15: Quiz 10.7 to 10.9
Day 16: Random Sampling
Day 17: Margin of Error
Day 18: Observational Studies and Experiments
Day 19: Random Sample and Random Assignment
Day 20: Quiz Review (10.10 to 10.13)
Day 21: Quiz 10.10 to 10.13
Learning Targets
Use the properties of special quadrilaterals to decompose shapes into rectangles and find their area.
Connect the dimensions of the original shape to the base and height of a rectangle to generate an area formula for parallelograms, trapezoids, and rhombi.
| Tasks/Activity | Time |
|---|---|
| Activity | 25 minutes |
| Debrief Activity with Margin Notes | 10 minutes |
| QuickNotes | 5 minutes |
| Check Your Understanding | 10 minutes |
Activity: Cut and Paste
Lesson Handouts
Media Locked
Media Locked
Answer Key
Media Locked
Homework
Media Locked
Additional Media
Media Locked

Experience First
Now that students have made important observations about the diagonals of several quadrilaterals, we’re ready to apply these properties to finding their areas. First, we remind students that finding an area is nothing more than determining, by counting, or some other strategy, how many unit squares make up an object. For rectangles and squares this is easy, but what if we don’t have full squares? Students investigate this first on a coordinate grid where they may combine partially shaded boxes to make full boxes or take off the triangular part and arrange it on the other side to make a rectangle. Then students start investigating other shapes. Each group will need several copies of each shape. Since there are two per page, we recommend printing two copies of the whole document for each group, so students have four copies of each shape. They will also need scissors. Using the constraint that they can only make 2 cuts, we ask students to turn a parallelogram, trapezoid, and rhombus into a rectangle and apply the rectangle area formula of base x height.
There are multiple ways students can go about doing this, and seeing the different strategies always proves to be very interesting to students. Below we’ve shown some different ways to rearrange a trapezoid into a rectangle. Though students may use different dimensions to determine the “base” and “height”, their final area will be the same. Are there other methods? A key question to ask students as you monitor groups is why the triangular piece of the parallelogram, for example, fits perfectly onto the side of the parallelogram. It is important for students to make use of the parallel lines of the bases to identify the congruent corresponding angles. Later in question 6, they will see that if no sides are parallel, the path to making a rectangle is not as clear cut because congruent angles are not guaranteed. Question 5 is aimed at getting students to see which dimensions on the original shape make up the “base” and the “height” of the new rectangle. We want students to look for the perpendicular measurements, which in the case of a rhombus, are the diagonals.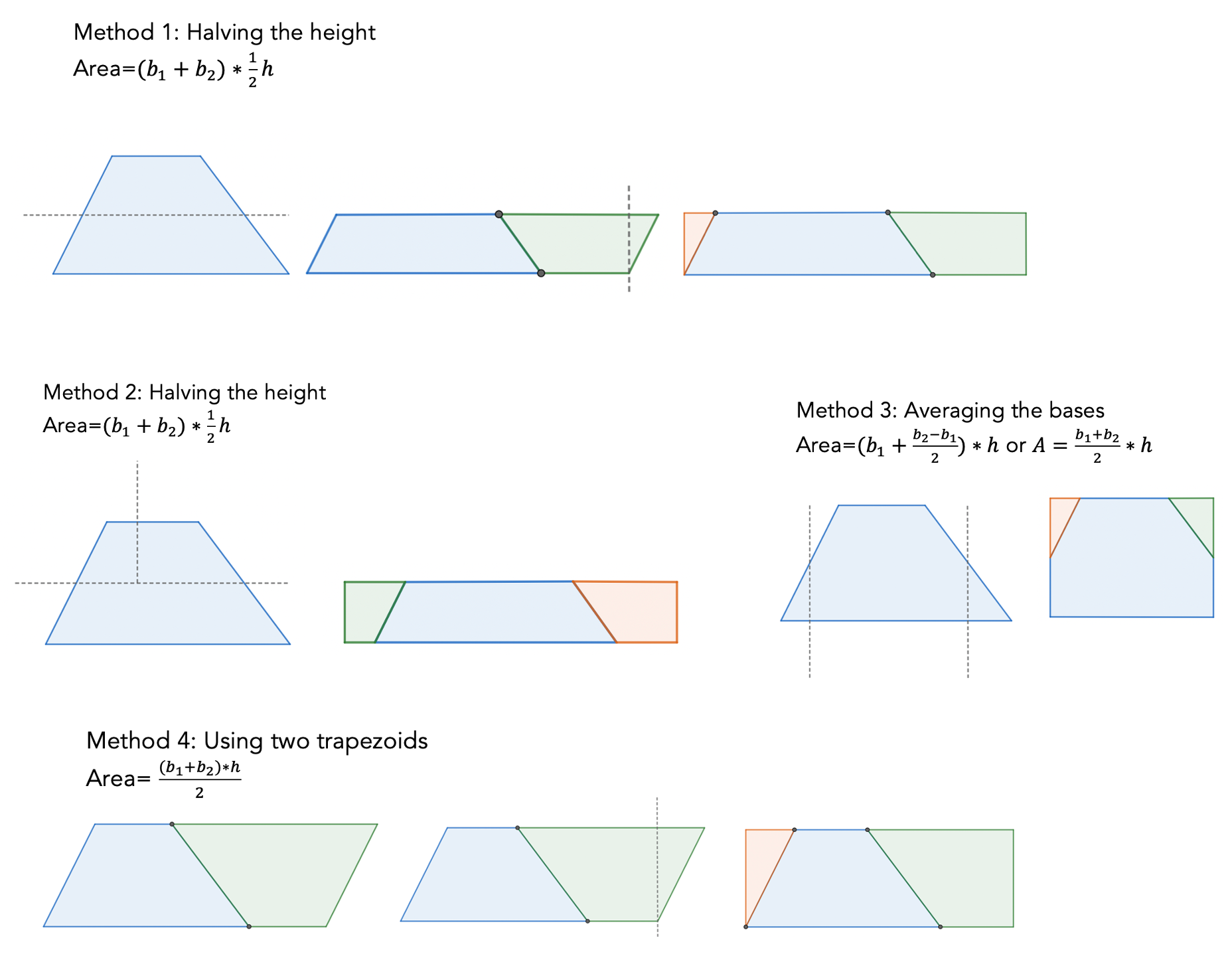
Formalize Later
While finding the area of 2-d shapes is generally its own chapter in a Geometry book, this is a skill students should already have familiarity with from the middle grades. Instead of covering each shape on a different day, we ask students to think creatively about how any trapezoid or parallelogram can be turned into a rectangle by making use of its properties. Since students are already comfortable with the idea of finding the area of a rectangle by multiplying the base by the height and that base and height are perpendicular, we want students to see that they can use this formula for other shapes as well, as long as they clearly define what the base is and what the height is. Furthermore, students review that decomposing and recomposing shapes does not affect area and is a useful strategy for finding the area of non-rectangles. The Check Your Understanding questions get at this further by asking students to come up with multiple ways to make certain areas or finding possible dimensions for the two bases given constraints. Instead of memorizing area formulas and applying them forwards and backwards, we want students to be able to make use of the properties of a shape to find its area. We will have an area and volume unit later in the year where we will focus more on real-world applications and reasoning with equations.