Written by Lindsey Gallas published 3 years ago
Did you know there’s more to a line than y=mx+b? Of course you did, you’re a math teacher. But do your students know that? And, more importantly, do they know why you might WANT to write a line a different way? Mine didn’t until I changed the way I taught linear equations.
I used to teach algebra in a very abstract, algorithmic way. We spent many class periods writing equations for lines. We’d calculate slope using m=(y2-y1)/(x2-x1), plug it in for m, then plug in a point and solve for b.
A lesson looked like this.

And while this wasn’t the most exciting hour of their day, my students got really good at writing lines in the form y=mx+b. They could probably have done it in their sleep (because some of them were actually sleeping).
So where’s the problem? Well, when we moved on to standard form (and don’t even get me started with point-slope!) it all fell apart. Students would use these other forms if and only if they were told explicitly to do so. Even then, they would write the equation using what they had memorized, but then convert it to slope-intercept form to graph it or answer questions with it. It wasn’t even that they understood slope-intercept form better, it was just that they had memorized it better.
Looking back now, I can see that there were two major problems. First, the questions I was asking were encouraging students to develop procedural fluency instead of conceptual understanding. Second, I was not creating any sort of motivation or need for understanding these new linear forms. Why might they want to know how to do this?
Both of these issues could be solved with one thing: context. Adding relevant contexts to my instruction completely changed the way students thought about slope, points, and linear relationships.
Building Intuitive Understanding Through Context
When we’re using a context, the goal is for students to think about the problem as they actually would if they were in the scenario. Take a look at how you can use context to help students calculate slope and find a y-intercept intuitively and without a formula from this lesson in our Precalc course.

Using contexts also creates a desire to use forms other than slope-intercept to describe a linear relationship, as you can see in this excerpt from a lesson on point-slope form from our Algebra 2 course.
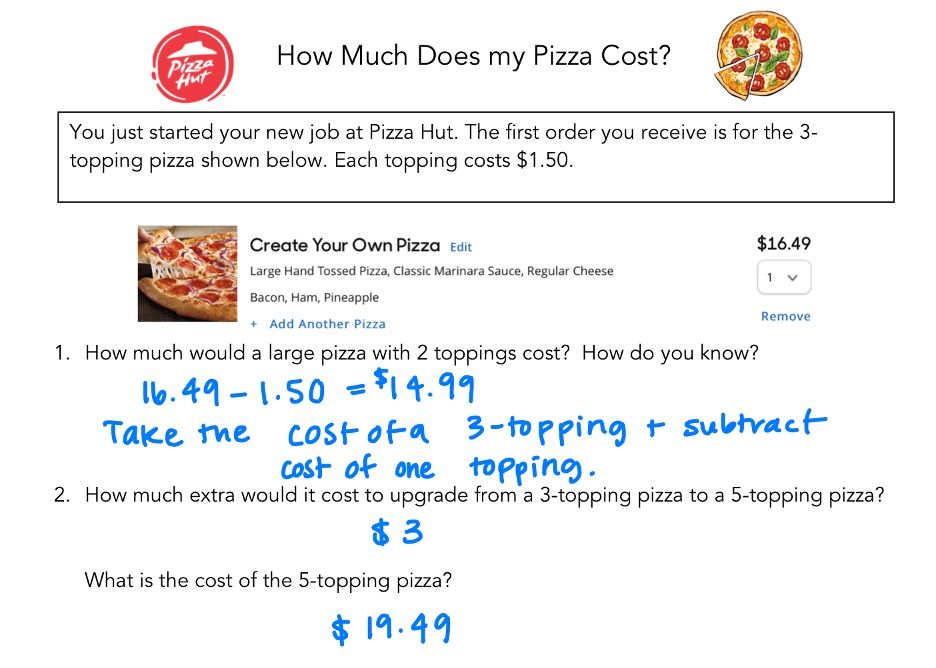
As you can see, the context is making the mathematical concepts that we want students to learn simpler and easier to understand. Once they have done the thinking within context, we can identify and formalize the concepts in the margins by adding generalized versions of their answers and academic vocabulary.
This approach might be a change for both you and your students. Your students may have been taught that contextual, or “real-world” problems require extracting the relevant information and turning it back into a standard problem to which they can apply a known set of procedures. Context, in this scenario, becomes an additional layer of complexity requiring decoding, instead of a helpful tool for understanding the underlying mathematics.
We think that context should be used to highlight the mathematical concepts, not obscure them. Context, when incorporated thoughtfully, prompts students to use intuition and background knowledge to make sense of new problems instead of relying on memorized algorithms.